1. 분포란?
분포(distribution)는 흡수된 부위에서 인체의 다른 부위로 이동되는 과정을 말한다.
흡수가 진행될 때 화학물질(생체이물)은 흡수장기(피부, 폐, 위장관)의 세포 인접부위에서 해당 장기의 간질액(interstitial fluid, 사이질액, 세포를 둘러싸고 있는 액체)으로 이송된다. 간질액이 나와서 첨언하자면, 체액에는 전체 체중의 40%를 차지하는 세포내액(intracellular fluid, 세포 안에 존재하는 액체)와 체중의 8%를 차지하는 혈장(blood plasma)이 있다. 그러나 이 체액들은 서로 나뉘어 있는 것이 아니라 혼합되어 있다는 점을 전제로 알아두길 바란다. 주로 순환계에 의해 분포되지만 림프계를 통해서 분포되기도 한다.
2. 겉보기 분포용적
만약 독성물질이 혈장으로 들어가면 혈액은 심혈관 순환계(cardiovascular circulatory system)를 통해 체내에서 신속히 이동할 것이다. 이 혈장에서의 생체이물 수준은 작용부위에서 독성물질의 농도를 결정한다. 즉, 작용부위에서의 독성물질 농도를 알 수 있게끔 독성물질이 포함된 체액의 총 용적(물건을 담을 수 있는 부피)을 겉보기 분포용적(apparent volume of distribution, Vd, d는 아래첨자)라고 한다. 이 Vd는 리터로 표시한다. Vd가 크다는 것은 약물이 온몸에 광범위하게 분포하고 있거나, 어떤 조직에 고농도로 분포함을 의미한다. 즉 Vd는 약물이 신체에 분포하는 정도와 그 농도에 관련된 값이다. 이는 체내 약물의 양을 안다는 전제 하에 혈중 농도를 예측할 때, 혹은 원하는 혈중 농도에 도달하기 위한 투여 용량을 산출할 때 유용하게 사용된다. 주의해야 할 점으로는 이 분포용적이 약물의 조직분포 정도에 대한 정보를 주기는 하지만, 약물이 어디에 분포하는가를 알려주지는 않는다. 그러므로 감염 부위 및 그 약물이 감염부위에 얼마나 잘 침투하는가에 대한 세부 정보를 아는 것이 중요하다.
Vd는 (약물의 투여용량) ÷ (혈중농도) 로 구할 수 있다.
약물을 투여하면 약물 농도는 곧바로 증가하며,혈액에서 조직으로 분포됨에 따라 혈장농도는 감소한다. 초기에 많은 용량을 투여하는 부하용량(loading dose)의 목적은 약물이 치료에 효과적인 혈장 농도에 빠르게 도달하도록 하는 데 있다. 생명을 위협하는 상황에서는 초기에 부하용량을 늘려 투여한다. 부하용량 이후에 투여하는 용량을 유지용량(maintenance dose)이라고 하는데, 이 때 조직과 혈장 사이의 약물농도는 평형상태가 된 것이므로 용량을 줄여서 투여한다. 유지용량은 바람직한 항정상태(steady state)의 혈장 농도를 유지한다.
부하용량 = Vd × 항정상태 농도
유지용량 =제거율 × 항정상태 농도



3. 초회통과효과(초회통과대사)
생체이물을 경구로 투여하게 되면 상당량이 순환계 대신 간으로 먼저 운반된다. 약물이 간에서 대사될 경우 전신 순환에 도달하는 약물(대사체가 아닌 활성을 가진 처음 약물)은 처음 흡수되었던 약물량 보다 상당히 감소하게 된다. 이 현상을 초회통과효과(first pass effect, first pass metabolism)라 한다. 예를 들면 혈압약 한 알에 100분자가 있다고 치자. 그런데 이 약 1정을 경구로 복용한뒤에 약이 위장으로 내려가면 이 분자들이 순환계통에 들어가기 전에 간으로 이동하게 된다. 간에서는 이 약의 70%, 즉 70분자를 해독하게 되고, 결국 나머지 30개가 혈액 중에 떠다니며 본연의 역할을 하게 되는 것이다. 단 이 초회통과효과는 경구투여일때 해당된다는 점을 명심하자. 폐와 피부를 통해 흡수되는 독성물질은 혈액으로 들어가 곧바로 순환계로 진입한다. 정맥이나 근육 주사제도 역시 마찬가지다.

4. 구획모델(분포모델)
먼저 구획(compartment)에 대해서 말해보자. 약물이 체내 성분과 결합하여 조직에 축적되면 그 조직은 저장 공간으로서의 역할을 할 수 있다. 이 저장되었던 약물은 혈중 농도와 평형을 이루고 있다가, 혈중 농도가 떨어지면서 비로소 조금씩 용해되어 나오게 된다. 구획(compartment)은 이러한 유사한 조직이나 체액의 군을 말하는 것으로서, 특정 조직을 일컫는 것은 아니다. 즉, 구획은 약물분포가 비슷한 장기나 조직을 말한다. 혈액이 많이 흐르는 구획(central compartment)으로 혈액, 신장, 폐, 간, 심장을 들 수 있으며 말초구획(peripheral compartment)으로서 지방조직, 근육조직, 뇌척수액이 있다.
구획모델(Disposition model)은 시간이 변함에 따라 체내에서 독성물질이 어떻게 움직이는지를 묘사할 때 사용된다. kinetic model로 알려져있기도 하다. 이 구획모델들은 1구획 모델(one-compartment open model)이나 2구획 모델(two-compartment open model), 다구획 모델(multiple compartment model)로 구성되어있다.
1구획 모델(one-compartment open model)은 약물 투여 후 즉각적으로 체내 전체에 약물이 분포되는 것으로 가정한다. 가장 자주 쓰이는 모델이며, 대표적으로 아미노글리코사이드계 항생제가 있다.

이 물통이 우리의 환자라고 가정해보자. 이 물통 안에 약을 넣는 즉시 약은 바로 물통 구석구석까지 퍼진다. 그 후 시간이 지나면 물통 부피 전체에 균일하게 분포하게 될 것이다.
그 다음엔 약이 일정한 농도 비율로(원: constant concentration-dependent rate) 해당 물통 부피 안에서 제거된다. (즉, 모든 임의 시간 단위에 대해 약물의 50%가 구획으로부터 제거된다).

사실 이 그래프는 현실에서 나올 수 없는 그래프다. 허나 모델로서는 충분히 가치 있는 사고 실험이라는 것을 알아두자. 이 모델에서 알 수 있는 것들이 있다. 첫째, 시간이 0일 때의 부피가 바로 앞서 말했던 겉보기 분포용적인 Vd다. 이 약의 경우 1g/L이다. 둘째, 약이 제거되는 속도는 제거에 대한 비율 상수, 즉 제거 속도 상수로 설명된다. 이 경우 k=0.5(즉, 약물의 50%가 단위 시간 당 제거된다). 보통 k에 사용되는 시간 단위는 1분이다. 클리어런스(단위 시간당 약물이 제거되는 혈장의 부피)는 k ×Vd 라는 방정식으로 설명된다.
2구획 모델(two-compartment open model)은 약물이 혈액에 많이 관류하는 중심구획으로 빠르게 분포한 후 느린 속도로 다른 장기에 분포한다고 가정한다. 평형을 유지하기 위해 두 구획 사이를 이동한다.
아까와 같이 같은 구획에 같은 용량의 약을 투여하자. 여기서 투여한 구획을 central compartment, 즉 혈액이 많이 흐르는 구획이라고 말한다. 이 central compartment 이외에도 우리 몸에는 말초구획(peripheral compartment)이라는 것이 있다. 해당 약이 앞서 그랬듯이 빠르게 모두 분리되어 central compartment로 들어가게 되어도, peripheral compartment(말초 구획) 사이를 평형을 유지하기 위해 이동한다.
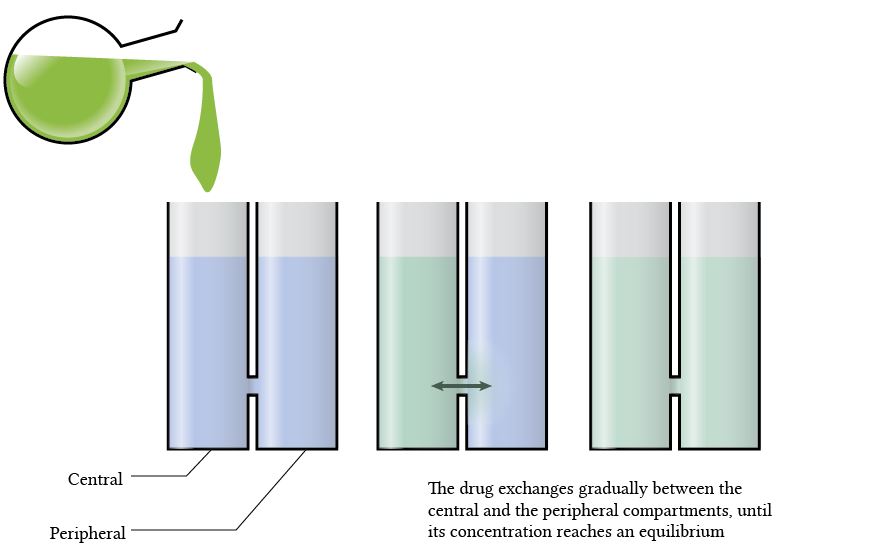
각각의 구역이 1L 만큼의 부피를 차지하고 있고, 확산 속도가 0.1이라고 생각해보자. (10%의 central compartment 약은 말초구획을 한 번 이상 왕복할 것이다.) 만약 ‘제거’(원: elimination)를 할 수 없게 되면, 두 구획은 농도평형에 도달하게 된다. 만약 예시의 central compartment를 실제로 조사해볼 수 있다면 그 약의 농도는 0.5g/L가 나올 것이다.

이는 모두 ‘제거’가 일어나지 않기 때문에 발생한다.
두 구획 사이에서 확산되는 속도가 제거되는 속도보다 빠르다고 가정해보자. 농도그래프가 앞서 봤던 것과는 다른 경향을 띨 것이다.


전체적인 그래프 모양이 다르다. 그 중 눈에 띠는 차이점은 바로 distribution phase와 elimination phase의 유무인데, 2구획 모델에서는 1구획 모델과는 다르게 central compartment concentraion 그래프에서 distribution phase와 elimination phase의 구성을 엿볼 수 있다. 곡선의 초기 가파른 부분을 distribution phase라고 한다. 조직 내 약의 분포가 혈장 농도의 빠른 감소를 결정하기 때문에 distribution phase라고 한다. 시간이 흐르면서 혈장과 조직 내 약물 분포가 점점 보다 많은 구획에서 농도평형을 이루게 되고, 마지막으로는 혈장 농도 변화가 '모든' 조직 내 약물의 농도에 비례적인 변화를 이룬다. 이 비례 단계에서 혈장 농도가 감소하는 것은 오로지 체내에서 약물을 제거하기 때문에 일어나는 일이다. 즉, 혈장 농도의 감소가 약물의 제거 운동과 일치한다는 말이다. 따라서 이 단계를 elimination phase라고 부른다.
1구획, 2구획 원문
The single compartment model
Behold, a bucket.

This bucket is your patient. Into this bucket, a drug has been added. The drug is instantly and completely dispersed to every corner of the bucket and is thereafter homogeneously distributed throughout the volume.
It is then eliminated from this volume at a constant concentration-dependent rate (i.e. for every arbitrary unit of time 50% of the drug is cleared from the compartment).

Clearly, this is not what happens in clinical reality, but as a model this is a valuable thought experiment. It illustrates some important concepts. The volume at time zero is the volume of distribution (Vd) - for this drug that volume is 1g/L. The rate of elimination is described by the rate constant for elimination, k. In this case k=0.5 (i.e. 50% of the drug is eliminated from the compartment per unit time). Classically, the unit of time used for k is one minute. The clearance (Cl) of the drug from this single compartment is therefore described by the equation (k ×Vd).
There are whole drug classes for which pharmacokinetics are well predicted by a single compartment model. For example, highly hydrophilic drugs which are confined to body water usually have single-compartment pharmacokinetics. Aminoglycosides are an excellent example. They have barely any tissue penetration and are essentially confined to the extracellular (in fact, intravascular) fluid volume.
However, virtually none of the anaesthetic drugs which you will use can be accurately described by this model. Let us now complicate things by adding another compartment.
The two-compartment model
Again, the same dose of drug is administered into the same compartment. Let us call it the "central" compartment. There is now also a "peripheral"compartment in the system. Though the drug is still distributed instantly and homogeneously into all of the central compartment, it now also diffuses gradually into (and out of) the peripheral compartment.
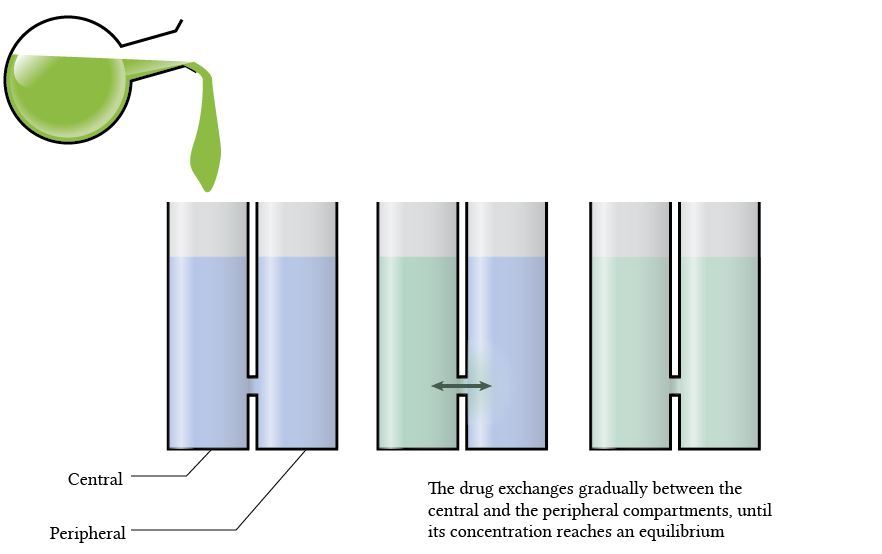
Let us assume that each compartment has the volume of 1L. Let the rate of diffusion again be something like 0.1 (i.e. 10% of the central compartment drug will have diffused into the peripheral compartment over the course of one unit of time). If there is no elimination taking place, the compartments will achieve an equilibrium. If we were to sample the central compartment, the concentration of the drug will be measured as 0.5g/L.
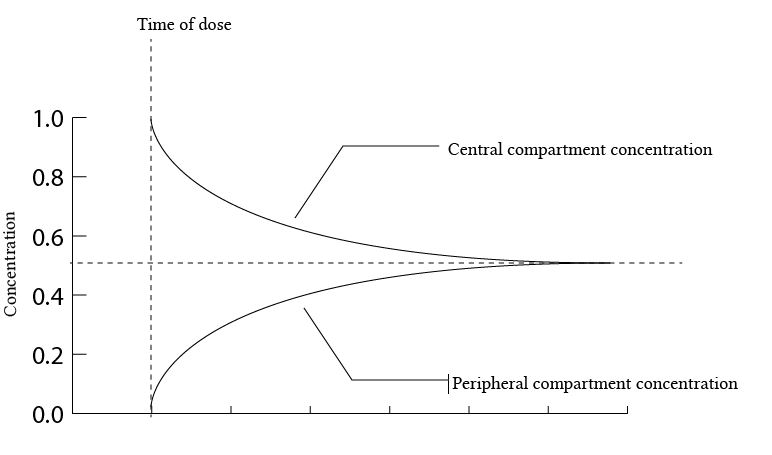
This is all in the absence of elimination. If the drug was being cleared from the central compartment at a concentration-dependent rate, more complexity is introduced into the model. Let us now assume that the rate of diffusion between compartments is more rapid than the rate of elimination. The concentration graph will now have two distinct phases: rapid initial distribution and slow late elimination.

This leads us to the familiar-looking graph of the bi-exponential decline, with two distinct phases of change in drug concentration:
- The distribution phase is the initial rapid decline in serum drug concentration
- The elimination phase is the slow decline in drug concentration, sustained by redistribution of drug from tissue stores.
One can see how this modeling lends itself to ever-increasing complexity. Considering that every little lacuna of fluid in the human body can be viewed as its own individual compartment, one can go quite mad trying to accurately model pharmacokinetics. For the purpose of preserving sanity, one needs to simplify this into something easily grasped by the human mind. For example, practically speaking in anaesthetics there is usually only need to consider three compartments: blood, lean tissues and fat.
The initial steep phase of the curve is called distribution phase because distribution into tissues primarily determines the early rapid decline in plasma concentration. With time, distribution equilibrium of drug in tissue with that in plasma is established in more and more tissues, and finally (during the linear phase in the semi-logarithmic plot) changes in plasma concentration reflect a proportional change in the concentrations of drug in all tissues and therefore in the amount of drug in the body. During this proportionality phase, the body acts kinetically as a single compartment. During this phase, the decline of the plasma concentration is associated solely with elimination of drug from the body, in other words it corresponds to the kinetics of drug elimination. Therefore, this phase is often called the elimination phase.
5. 분포를 방해하는 요인들
기관과 조직들은 각각 받거나 노출되는 화학물질의 양이 다르다. 그 원인으로는 크게 두 가지가 있다.
1. 특정 조직을 통과하여 흐르는 혈액량의 차이
2. 체내 독성물질 출현을 감소시키기 위한 특별한 장벽의 존재
보다 많은 혈액이 흐르는 기관들은 잠재적으로 독성물질을 더 많이 축적시킬 수 있다. 여기에 해당되는 신체기관으로는 간, 신장, 뇌전근, 뇌가 있다. 뼈와 지방조직들은 상대적으로 낮은 혈류 속도를 가진다. 하지만 여기에도 예외가 있는 법. 그 예외가 바로 조직친화력(Tissue affinity)다. 몇몇 조직들은 특정 화학물질에 대해서 높은 친화력을 지니고 있어 낮은 혈류 속도에도 불구하고 높은 농도로 물질이 축적될 수 있다. 예를 들자면 지방 조직이 있다. 이 지방조직은 낮은 혈류 속도에도 불구하고 지용성 독성물질이 축적된다. 5번 주제와는 벗어난 얘기지만 첨언하자면 혈류 속도가 약물이 빠져나오는 속도에 영향을 미쳐 약물이 혈관이 풍부한 조직, 근육조직, 지방조직 순으로 빠져나간다.
구조적인 장벽(Structural barrier)은 특정 기관이나 조직에 들어가려고 할 때 말 그대로 구조적인 장벽에 가로막혀 침투하지 못하는 것을 의미한다. 뇌, 고환, 태반에 존재하고 있다.
뇌에 있는 장벽은 혈액-뇌장벽(Blood-brain barrier)이라고 하는데, 성상세포(astrocytes)라고 불리는 세포들과 인접한 내피 세포 사이의 지방에 수용성 분자들의 통과를 제한한다. (성상세포는 모세관 내피 세포층과 뇌의 신경세포 사이의 벽을 형성하는 많은 작은 돌기들을 지니고 있다. 중추신경계에서 패킹 조직을 형성하는 신경교세포다.) 이 장벽이 만능은 아니지만 산소를 포함한 필수 영양소들은 들여보내는 한편 독성물질들의 속도를 현저하게 낮춘다.
자료조사 출처
http://www.bosa.co.kr/news/articleView.html?idxno=2011944
제2장 약물 - 의학신문
장시간 작용 제제 장시간 작용하는 제제의 제제화는 제형 설계에 있어 상당한 진보라 할 수 있다. 장시간 작용하는 제제는 투여...
www.bosa.co.kr
https://www.youtube.com/watch?v=BQQns7RAUzA
http://doctorkorea.com/pharmacology/index_in.asp?no=10&id=8861&c3_idx=254&c4_idx=632&title=%C7%D5%B8%AE%C0%FB%C3%B3%B9%E6
약물의 투여경로 1. 경구투여 (oral administration, po) 경구투여는 가장 자연스러운 투여법으로 투여가 용이하고 안전하며 다량의 약물 투여시 편리하고 경제적이다. 약물의 흡수는 거의 소장에서 이루어지나, 위와 대장에서 흡수되는 약물도 있고 팽창성 하제와 같이 소화관에서 흡수되지 않고 작용을 나타내는 약물도 있다. • 경구투여의 단점 ① 위장내용물의 종류,양에 따라 흡수의 차이와 약효가 일정하지 않다. ② 소화액에 의해 약물이 불활성화되는
doctorkorea.com
https://blog.naver.com/yanni425/220113328165
[경피독 3] 간 초회통과효과 Liver first-pass effect
경피독은 피부를 통해 흡수되는 독 이라고 하였습니다. 경피독이 무서운 이유는 간 초회통과효과를 받지 않...
blog.naver.com
https://blog.naver.com/hafs_snu/220860114813
[대학교 일반화학]반응속도(Reaction Rate)/초기 반응속도(Initial Rate)/속도상수(rate constant)
by. 두턱괴물 우리는 앳킨스 14장을 공부할 것이예요~ 여태까지는 평형을 공부했다면, 이제는 평형 다 잊어...
blog.naver.com
https://blog.naver.com/drugum/221382079458
약대생블로그) 약동학(pharmacokinetics) 정리
으.. 내가 정말 싫어했던 약동학 원컴, 투컴 모델 등등.. 계산하는 문제가 많이 나와서 별루 안좋아했다. ...
blog.naver.com
https://jiyun928.blog.me/221112058450
https://sepia.unil.ch/pharmacology/?id=93
Distribution and Elimination phase
Time course of the plasma concentration of a drug applied by a single i.v. injection.
sepia.unil.ch
https://terms.naver.com/entry.nhn?docId=150042&cid=50317&categoryId=50317
성상세포
중추신경계에서 패킹 조직을 형성하는 신경교세포.
terms.naver.com
https://blog.naver.com/jjj_1/221182371681
3.약동학 pharmacokinetics
약물은 약효를 나타내는 농도로 표적기관에 도달하여야 한다.우리 인체가 이물질이나 독성물질로부터 보호...
blog.naver.com
https://ko.wikipedia.org/wiki/%EC%95%BD%EB%AC%BC%EB%8F%99%ED%83%9C%ED%95%99
약물동태학 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 효소와 기질 사이에 미하엘리스-멘텐_식을 만족하는 관계를 보이는 모델을 나타낸 그래프: 기질이 약제학적 약물일 때 약물동태학에서 연구하는 하나의 파라미터이다. 약물동태학(藥物動態學, 영어: pharmacokinetics PK, 약동학, 약물체내속도론)은 약물의 흡수, 분포, 대사, 배설과정을 동역학적 관점에서 해석하고[1] 예측하고자 하는 약물학의 세부 학문이다. 영문 Pharmacokinetics는 고대 그리스어로 약물
ko.wikipedia.org
http://gogle.clinic/psychiatric-pharmacokinetics/
분포 어렵네요... 구획 모델 나오고 뇌 멈춤
*해당 내용은 전문 지식이 없는 중학생이 작성한 것입니다.
'독성학' 카테고리의 다른 글
| 2. 독성동태학-배설(excretion) (0) | 2019.08.21 |
|---|---|
| 2. 독성동태학-생체내변환(biotransformation) (0) | 2019.08.15 |
| 2. 독성동태학-흡수(absorption), 확산(diffusion) (0) | 2019.08.12 |
| 2. 독성동태학-서론 (3) | 2019.08.12 |
| 1. 기본원리-독성작용 (0) | 2019.03.24 |



